Research items

By using the variational principle based on the discrete differential geometry formulated by Kajiwara Group, we develop optimization methods to model the surfaces (manifolds) of various functions needed not only in the design of architecture, but also in the structural optimization, the response approximation and the parameter identification through the following three items.

1. Methods to generate the surfaces with mechanical rationality and artisticity based on the geometry of piecewise smooth surfaces.
2. Methods to design the curved surface structure with “aesthetic shape.”
3. Methods of analysis, identification, and optimization for the “safe and secure” architectures based on the piecewise smooth high dimensional manifolds.

Outline

1. To design the curved roof surface or the façade (exterior appearance), the key point is the method of design of piecewise smooth surfaces based on various geometric or aesthetic shape metrics. To this end, extending the technique of the Ricci flow, which has been already in practical use in the field of CG, we establish the methods to design the surfaces based on the variational principle and the invariants in the discrete differential geometry. This is carried out by developing efficient algorithms to generate piecewise smooth surfaces or surfaces that approximately satisfy the constraints of aesthetic shape metric or geometric constraints. We also develop the parametric representation of surfaces replacing NURBS by defining the piecewise smooth surfaces using the new basis curves, such as the aesthetic curves. Then we propose a method of designing the curved surfaces in architecture by using the shape models that can easily formulate the invariants to represent “beauty and artisticity”.
2. The membrane structure covering a large space of architecture is generated from the plane membrane sheet, and it is desirable to be in the uniform tension state after construction. To this end, it is preferable that surface has an intermediate shape between the developable surface and the minimal surface. To design such surfaces, we derive the relationship among the deformation within the membrane, the invariants of the surface shape, and the tensile force in self-equilibrium state, and propose a method based on the variational principle to optimize the surface shape within the specified deformation. Such problems will be formulated as the multi-objective optimization problem using the definition of the distance between the discrete surfaces proposed by Kajiwara Group. Also, we quantify the shapes of curved roof surface of architecture formed by the rigid-foldable polygons and propose the method to design the rigid-foldable roof structure, which is close to the developable surface. We characterize the piecewise smooth surfaces constructed by piecewise-developable surfaces divided by curves based on the variational principle allowing the singularities on the whole surfaces, not by connecting the developable surfaces. This enables the design of the aesthetically pleasing shapes with security and safety, since it improves the mechanical stiffness and makes the optimization of other mechanical properties feasible.
3. We extend the discrete differential geometry for designing surfaces to generate the approximate surfaces representing the deformation of structures under external loads. We then apply it to propose new basis functions, design of structures with specified deformed shapes, automatic generation of the similar designs using the relationship between the invariants of the response distribution and features of the design. Also, the approximate function may be regarded to form the high dimensional manifold in the data-driven approaches to directly predict the constitutive relation from the results of the material tests. So far, the smooth manifolds have been used to approximate such functions and relations; however, we propose a new prediction method by formulating the smoothness and distance based on the discrete differential geometry allowing the class of piecewise smooth surfaces. Finally, we generalize the methods of designing the piecewise smooth surfaces based on the variational principle.

Placement in the project

This group consists of the researchers in architecture and mathematical engineering, and develops the methods to implement the basic theory of shape generation and distance metric, which use the various invariants of the discrete differential geometry proposed by Kajiwara Group. We remarkably improve the accuracy of approximation of the various functions (manifolds) in the structural analysis and optimization by the approximate surfaces using the piecewise smooth surfaces.

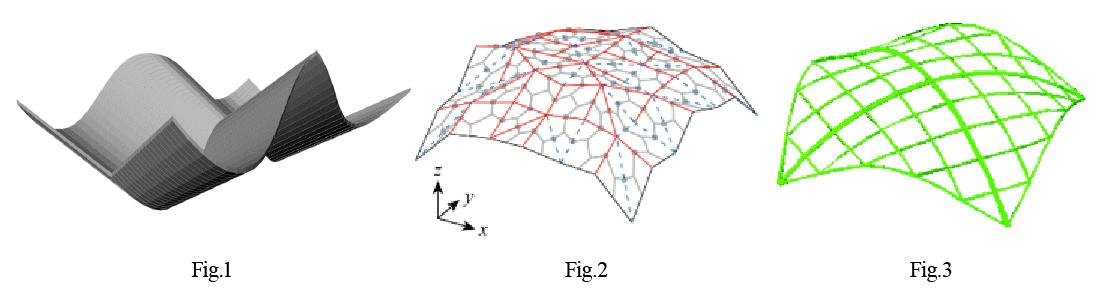
So far, we have proposed the shape optimization methods using the fairness metric of the surfaces and geometric invariants. We also have the method of optimum design of the architectural curved surfaces as an assemblage of developable surfaces (Fig.1), and the method to design the membrane structure with intermediate surfaces between the developable surfaces and the minimal surfaces. Moreover, we studied the method to design the curved surfaces with the rigid-foldable origami (Fig.2), and the gridshell consisting of discrete elasticae. It is indispensable for achieving the goals of the whole project to extend such researches to construct the novel framework of the architecture surface design based on the discrete differential geometry. Also, our new studies on the application of machine learning to optimal design and constitutive laws of materials are expected to lead to the response prediction by the discrete differential geometry and the parameter identification.