EDDDGE EDDDGE

EN

研究内容

研究内容

研究内容

I.新しい離散的な曲面論の構築
  1. 区分的に連続な曲面の幾何学。形状要素として通常平面四角形要素を取る離散微分幾何を拡張し、NURBS曲面や離散曲面を包摂する、離散と連続両方の性質をもつ区分的に連続な曲面のクラスを定義します。このクラスの曲面に曲率などの基本的な概念を導入し、離散変分原理などの解析手法を構築します。特に、施工性の観点から設計におけるニーズが高い、ガウス曲率が0である可展面を形状要素として取り上げ、設計実務から動機を得て理論を展開します。
  2. アート性が高い形状を効率的に設計可能にする「美的曲面」の理論。形状要素として、工業意匠設計分野で研究されてきた「美的曲面」を取り上げて理論を深めます。美的曲面の基盤となる対数型美的曲線(LAC)を、ユークリッド幾何におけるオイラーの弾性曲線のクライン幾何の一つである相似幾何における類似という枠組みを採用し、相似幾何における曲面論の枠組みで美的曲面を導入します。
  3. 幾何学的によい性質や力学的に優れた特性を持つクラスの曲面の理論。Willmore曲面を始めとする他のクライン幾何における極小曲面の力学的特性を解明して、設計に活かします。また、力学的特性に優れるとされる曲面、例えば測地線で張られる曲面などを変分原理で特徴付けて幾何学的な性質を解明し、より広い範囲の設計に活かすための基盤を構築します。
II. I.の数学的枠組みに基づいた設計法の構築と双方向循環型設計プラットフォーム開発
  1. 曲面の新しいパラメトリック表現と幾何的制約をみたす区分的連続曲面生成法：美的形状尺度や力学的エネルギーなどに対する離散変分原理に基づく曲面設計法を確立します。
  2. 美的形状を有する曲面状建築の設計法：膜構造建築で要求される可展面と極小曲面の中間的な曲面や、可展面に近く剛体折り可能な屋根などの多面体形状の設計法を(i)の枠組みで開発します。特に、曲面形状の最適化問題を、区分的連続曲面の曲率の概念から得られる離散曲面の距離の概念を使って多目的最適化問題として定式化して解く手法を構築します。
  3. 区分的に滑らかな曲面の特徴量の作る幾何構造に基づく解析・同定と最適化手法：構造物に荷重が作用したときの変形応答量を設計変数の関数として予測したり、変形量を材料試験データから直接予想したりするデータ駆動型の問題に対して、離散曲面の距離の概念を用いて新しい予想手法を構築します。
  4. 施工性＋力学的合理性に優れた幾何的に性質のよい曲面構造
  5. 幾何的な汎関数の離散化の有限要素法への応用：離散微分幾何における離散微分形式を活用した新しい有限要素法を定式化し、座標に依存しない簡潔な定式化と構造解析手法を実現します。
  6. 対数型美的曲線のクライン幾何類似と実装
  7. クライン幾何による美的曲面類似と実装
  8. 曲面法線マップ画像に基づく区分可展面の生成技術：曲面の生成に欠かせない、法線マップ（ガウス写像）から曲面を復元する逆問題を、区分可展面を用いて実現する技術を開発します。
  9. 空間曲線での折りを含む可展形状の対話的設計法の構築：曲面を折ることで生じる折り目を含む幾何形状の離散表現とその対話的設計手法を開発します。折りの角度や折り目を明示的に指定する方法と（順方向目的型）、(h)で開発される法線マップを指定する方法（逆方向目的型）を組み合わせた手法を開発します。
III. 異分野融合による新しい設計技術と数理技術の開拓
  1. 折紙工学における曲線折りの仮設構造物等への応用：計算幾何学で発達した折紙工学の最先端の技術である曲線折りを建築設計に取り入れ、可搬性や剛性に優れた仮設構造物の設計に活用します。災害時の生活の質の向上に貢献できます。
  2. 可展美的曲面、膜構造美的曲面の提案と建築・造船への応用
  3. 可展面の連続変形とクライン幾何学的分析：可展面をガウス・コダッチ方程式を用いて解析し、特異点（折り目）周りの解の挙動を分析して折り目の推移過程を分析する理論的なツールを構築します。これを基盤としてクライン幾何の手法を活用して可展面の変形を記述し、表面積極小化問題を考察して可展面と極小曲面の中間に位置する新しい曲面族を生成します。

研究体制

以下の研究グループを編成し、グループ間で協力の下で研究を進めます。

メンバー

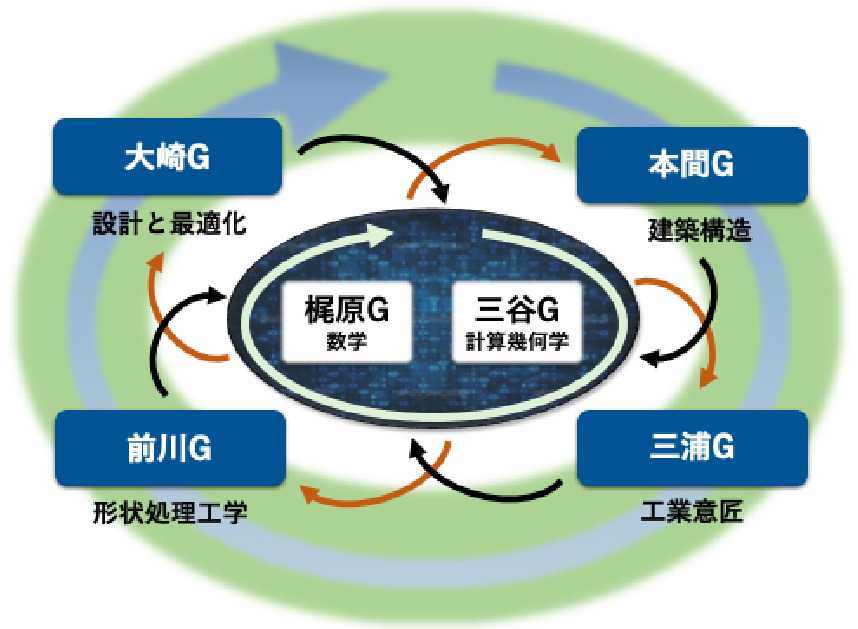
梶原グループ

代表者:
梶原 健司（九州大学）
主担当:
新しい離散曲面の幾何学　I.(a),(b),(c)

詳しくみる

大崎グループ

グループリーダー:
大崎 純（京都大学）
主担当:
離散微分幾何学の変分原理を用いた区分的に滑らかな曲面の設計と最適化 II.(a),(b),(c)

詳しくみる

本間グループ

グループリーダー:
本間 俊雄（鹿児島大学）
主担当:
施工性・力学的合理性に優れた建築構造 II. (d),(e), III. (a)

詳しくみる

三浦グループ

グループリーダー:
三浦 憲二郎（静岡大学）
主担当:
クライン幾何による意匠設計用自由曲線・曲面の定式化とその実務への応用 II. (f),(g), III. (b)

詳しくみる

前川グループ

グループリーダー:
前川 卓（早稲田大学）
主担当:
曲面法線マップ画像に基づく区分可展面の生成 II. (h)

詳しくみる

三谷グループ

グループリーダー:
三谷 純（筑波大学）
主担当:
空間曲線での折りを含む可展形状の設計法 II. (i), III. (c)

詳しくみる

研究の進め方

以上の研究体制で、以下のように研究を進めます。

  1. 各年度、3ヶ月に1度、研究代表者と主たる共同研究者が全員、および計画参加者のうち希望者が集まる戦略会議を開催し、研究情報を共有し、進捗状況の調整を図ります。
  2. 上記各年度4回のうち、2回は国内の計画参加者が集まる全体会議とします。
  3. 上記のうち1回は海外の計画参加者も参加する国際ワークショップとし、研究成果を発信します。
  4. 以上に加え、初年度にはキックオフミーティング、最終年度には国際研究集会を開催します。
  5. 2020年度ないし2021年度を目処に日本応用数理学会に「応用幾何学研究部会」（仮称）を設立し、大学院生や特別研究員などの若手研究者を含む、計画参加者の活動の場を安定的に確保します。

本研究プロジェクトに至るまで

日本では数学研究の純粋数学志向が強く、理論物理学以外の諸科学分野や産業界と研究に関して接する機会がほとんどない状況が続いてきました。九州大学マス・フォア・インダストリ研究所（IMI）はこの状況を変え、数学における産学・諸科学分野との本格的な連携研究を進めるために2011年に設立されました。研究代表者は数理物理学、特に離散可積分系の研究から2009年頃に離散微分幾何の研究にシフトし、2011年にIMIに配属されてからは離散曲線の可積分変形理論や離散正則函数の研究を通じて理論的な基盤を構築してきました。並行して以下のIMI公募制共同利用研究やコロキウムなどを企画・参加し、応用分野との接点を探ってきました。

  1. 短期共同研究「意匠設計のための微分幾何学・離散微分幾何」(2016.9.28-30)
  2. 短期共同研究「三次元幾何モデリング評価手法の提案とソフトウェア開発」 (2017.9.4-8)
  3. 短期共同研究「離散微分幾何の新展開：意匠設計から建築設計へ」 (2018.9.10-13）
  4. 短期共同研究「造船工学における曲面幾何」(2018.12.10-28)
  5. IMIコロキウム「建築構造における幾何学的諸問題」　大崎純（京都大）(2019.3.13)
  6. 短期共同研究「離散微分幾何の設計への応用：理論から実務へ」(2019.9.9-11)
  7. AIMaP研究集会「離散微分幾何と有限要素法の融合．建築とCGヘの応用」(2020.3.6-8)

美的形状の幾何については (1)で三浦と協働を開始、 (3)で一般的な離散微分幾何に関して三浦と本間、横須賀を含めた協働を開始しました。 建築設計については梶原グループが(5)に大崎を招聘、協働を開始しました。また、造船における諸問題については(2),(4)に梶原、鍛冶が参加し、理解を深めています。これら諸分野の問題意識を共有し協働を開始するため、(6)を実質的に第0回の戦略会議とし、ほとんどのグループリーダーが参加しました。 キックオフミーティングとして(7)を実施予定です。また、梶原グループに参加する離散微分幾何における世界的なリーダーのPolthierとは梶原、小磯が共同研究や大学院生の派遣などで交流を深めてきました。梶原グループの大学院生である軸丸芳揮、朴炯基がPolthierの元で3ヶ月間滞在して共同研究をしてきました。可積分離散微分幾何のパイオニアであるSchiefは、梶原と2016年から美的形状に関する共同研究を行っています。以上の活動とは独立に、三谷、前川、三浦は以前から緊密な研究交流があります。本研究プロジェクトはこれらの基盤の上に実施されるものです。

TOPへページの先頭へ