研究内容
三谷グループ
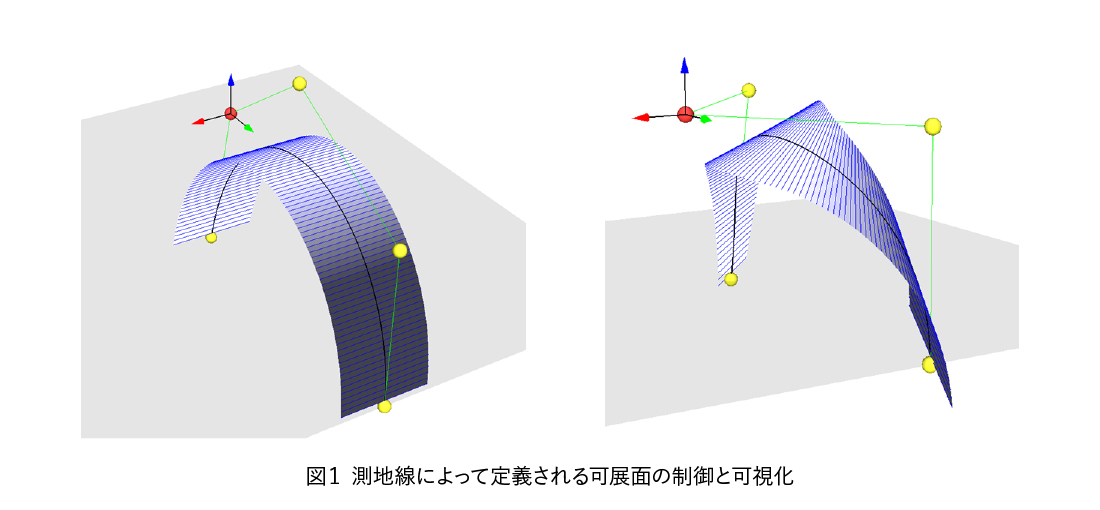
研究題目空間曲線での折りを含む可展形状の設計法
研究実施項目
折紙研究において重要な要素とされる「折り目」を含む形状について、その離散表現手法、および、対話的な設計手法の開発を行う。また、折り目が展開された状態から折られた状態への推移過程のモデル化を行う。さらに、折り目の推移過程を曲面の構造方程式の退化・型変化の観点から数学的に分析を行う。
- 折り目を含む可展形状の離散表現および対話的な設計手法の開発
曲面を折ることで生じる「折り目」を含む幾何形状の離散表現手法および、その対話的な設計手法について開発を行う。折りの角度や折り目を陽に指定する方法と、前川グループによる法線マップを画像で指定する方法を組み合わせた手法を開発する。 - 折り目が展開された状態から折られた状態への推移過程のモデル化
折り目における折り角度の変化によって素材が平坦な状態から、前項で表現された立体形状へと推移する過程をモデル化するための手法とともに、モデル化された形状および理論的な可展面モデル間の距離を定量化し、可視化する手法を開発する。 - 可展面の連続変形とクライン幾何学的分析
可展面は折り目(特異点)および臍点のない範囲で等温座標系とよばれる特殊な座標系でパラメータ表示が可能である。等温座標系で表示された構造方程式(ガウス-コダッチ方程式)の解が折り目でどのように退化するかをコンピュータシュミレーションを用いて分析し、前項の推移過程を解析的に記述する。同時にクライン幾何学的観点からも分析する。
研究概要
- 折り目を、空間曲線とその曲線に沿って定められる折り角度によって定義したとき、この曲線と、この曲線を境界として隣接する2つの曲面領域によって折り目を含む立体形状が構成される。2つの曲面領域は、それぞれ可展面であるとともに、平坦に開いた後でも隙間なく接続しなくてはいけない。そのため、このような幾何的な制約のもとで、どのように意図した形を設計するかが課題となる。微分幾何の観点からは、折り目は微分できない特異点としてみなすことができるため、このような性質を考慮した形状のモデル化を行うとともに、意図した形状を素早く得られるよう対話的な設計手法を構築する。また、対話的な操作手法をシステムに実装し、折り目を定義する空間曲線と折り角度、および平面に展開された状態における折り目の曲線(平面曲線)の指定と、得られる形状の確認をデザインプロセスに組み込むことを行う。
- 前項の形状設計において入力として与えられる平面上での折り目と、得られた折り角度によって構成される三次元形状を対象として、素材が平坦な状態から三次元形状へと推移する過程を、折り角度をパラメータとしたモデル再構成によって、その変形の過程を実代数幾何学的な手法を援用しつつ可視化を行う。しかしながら、平坦な状態から立体形状へ、可展性を維持したまま変形するパスが存在しない場合が考えられるため、変形過程においては、近似可展面モデルを用い、誤差を許容したモデルとして構築することを行う。また、この近似可展面モデルと可展面モデルとの距離関数を定義することで、製造工程における歪み量の推定と、その最小化を実現することを行う。
- 折り目をもつ曲面を構造方程式(ガウス-コダッチ方程式)の観点から分析し、特異点(折り目)のまわりでの解の挙動を分析し、前項の推移過程を解析的に記述する。三浦グループにより展開されるクライン幾何の手法を可展面に適用する。具体的にはラゲル幾何およびリー球面幾何とよばれる幾何学において可展面の変形を記述する。これらの幾何学における表面積極小化問題を考察することにより極小曲面と可展面を結ぶ曲面族を生成する。
研究構想における位置づけ
- 素材に対する折り加工で立体構造物を制作することは、産業分野において素材活用の効率化や加工コストの低減に貢献するとともに、素材の継ぎ目が無いことによる審美性の向上にも貢献する。本研究は、可展面の離散表現に折り目の数理モデルを追加することで、形状表現の自由度を高めるとともに、産業の効率化および審美性の向上に貢献するものである。
- 製造工程においては、素材の初期状態(平坦な状態に折り目が加工された状態)から、製品の最終形状までの変形過程を知ることは重要である。この過程に現れる形状は、必ずしも可展面として表現されるものには限らないため、可展面からの誤差を許容したモデルとして梶原・大崎グループの開発する近似可展面モデルを用い、素材に生じる歪みや応力などを可視化することを行う。
- 可展面と極小曲面を結ぶ中間的な曲面のクラスは、曖昧で特定する指導原理がない。本研究ではクライン幾何の着想で、ユークリッド幾何を越境することにより両者を結ぶ曲面族を生成する。大崎グループ・本間グループで求めている曲面族を生成する上で必須の研究に位置づけられる。またこの手法は三浦グループ・前川グループの曲面生成にも直結する。


 ページの先頭へ
ページの先頭へ