研究実施項目

1. 新しい離散的な曲面論の創出
2. 曲面に対する離散変分原理の構築
3. クライン幾何による美的形状の理論

研究概要

1. (a) 形状要素として通常平面四角形要素を取る離散微分幾何を拡張し、NURBS曲面や離散曲面を包摂する、離散と連続両方の性質をもつ区分的に連続な曲面のクラスを定義し、このクラスの曲面に曲率などの基本的な概念を導入する（予備的な成果は参考文献1., 2.を参照）。

   (b) 特異点（折り目）における曲率：建築において、複数のピース（板）をつなぎ合わせる時、つなぎ目をまっすぐな線分にするよりも曲がった曲線にする方が強度が増す。そこで、折り目に対してずれにくさ（強度）の指標となる汎関数を定義し、その臨界条件を用いて折り目の曲率を定義する。これは、特異点における曲率の定義の新しい考え方を与える。

   (c)「区分的連続曲面」の等長変形の理論を構築する。

   (d) 区分的連続曲面のクラスにおける距離を定義する。２つの曲面の間の実距離（ハウスドルフ距離など）に例えば曲率の差を表す量を加えることが有用であろう。



2. 区分的連続曲面のクラスにおける離散変分原理などの解析手法を構築する。

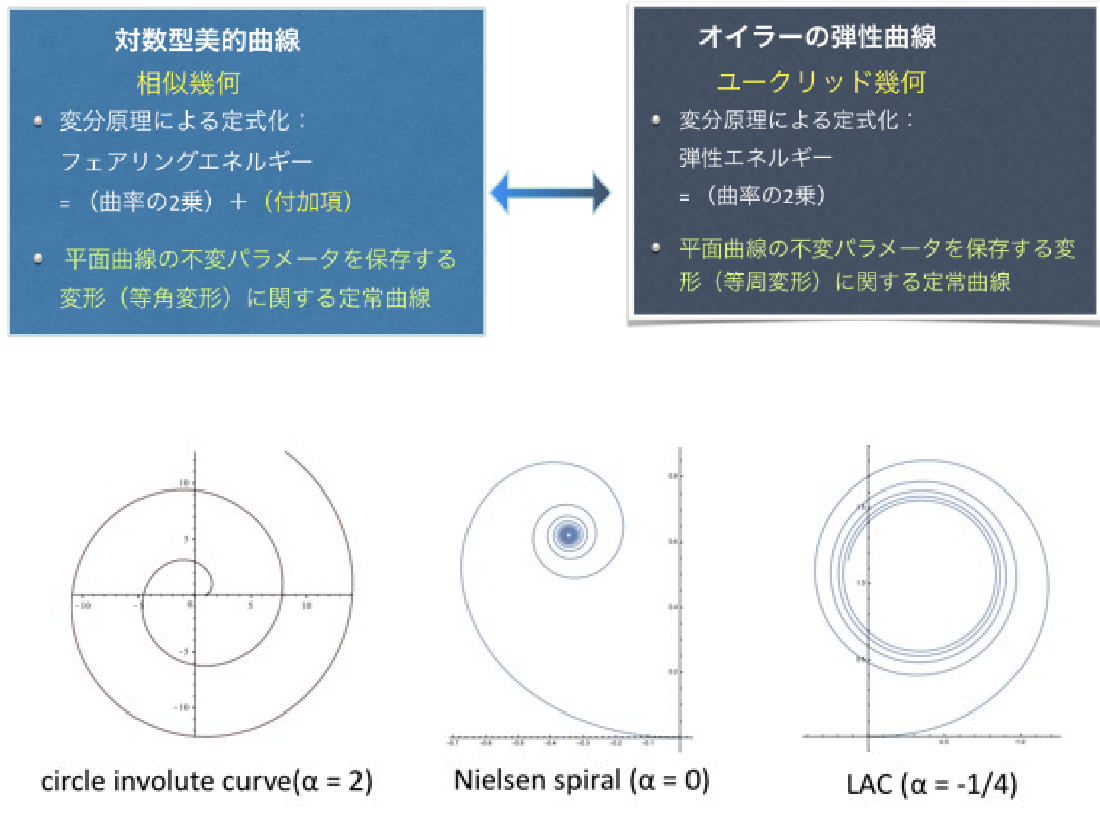
3. (a) アート性が高い形状の効率的な設計を可能にする「美的曲面」の概念を、クライン幾何の一つである相似幾何における曲面論の枠組みで考えるのが自然であるという観点により導入する。その発想は、美的曲面の基盤の対数型美的曲線が、ユークリッド幾何におけるオイラーの弾性曲線の相似幾何類似であるという枠組みを採用することにある（参考文献3.）。

   (b)美的曲面を曲面形状の最適化問題の解として捉えて解を求める理論を構築し、「美的形状」の設計を可能にする。

研究構想における位置づけ

本グループの研究は、本研究全体の課題遂行のための数学的基盤及び具体的な建造物設計のための基本的な方法を与える。すなわち、離散と連続両方の性質をもつ区分的に連続な曲面のクラスを定義し、そのクラスの曲面に対する変分法、特異点における曲率や法線などの幾何概念の有用な定義、等長変形の理論などの構築を行うことにより、新しい離散曲面の幾何学と新しい変分原理を創始・展開し、建築・設計工学・計算幾何学に提供する。さらに、曲線と曲面の幾何学に「美とアート性」という概念を導入することにより、「美とアート性」を備えた「安全・安心」な構造物を「効率的・低コスト」で設計することを可能にする革新的なプラットフォーム開発のための基礎理論を与える。 なお、個々の研究課題の遂行のために、他の全ての研究グループと協働する。

参考文献

1. M. Koiso. Uniqueness of stable closed non-smooth hypersurfaces with constant anisotropic mean curvature, preprint. arXiv:1903.03951 [math.DG]
2. Y. Jikumaru and M. Koiso. Non-uniqueness of closed embedded non-smooth hypersurfaces with constant anisotropic mean curvature, preprint. arXiv:1903.03958 [math.DG]
3. J. Inoguchi, K. Kajiwara, K.T. Miura, M. Sato, W.K. Schief and Y. Shimizu, Log-aesthetic curves as similarity geometric analogue of Euler’s elasticae, Computer Aided Geometric Design 61(2018) 1-5,
   https://doi.org/10.1016/j.cagd.2018.02.002.