研究実施項目

コンピュータ・グラフィックスにおける曲面や曲線の離散化に関する研究の発展は著しいものがあるが、曲面や曲線の曲率分布を制御する性質の良い幾何の建築への応用および普及については、未発達の段階である。特に境界形状を定める建築構造物は、離散変分問題が重要となる。ここに梶原グループや三谷グループとの協働により、新たな活用と構成方法を提案することができる。これにより、施工性・力学的合理性に優れた建築構造の設計手法を構築し、設計や施工の効率化と安全性の向上が期待できる。以下の研究実施項目を挙げる。

1. 施工性+力学的合理性に優れた幾何的に性質の良い曲面構造
2. 幾何的な汎関数の離散化と有限要素法への応用
3. 折り紙工学における曲線折りの仮設構造物等への応用

研究概要

以下に研究実施項目に対する研究概要を示す。

1. 1. 施工性+力学的合理性に優れた幾何的に性質の良い曲面構造

シェル構造や膜構造、張力構造といった力学的合理性に優れた構造形式は、主に軸応力や面内応力の抵抗により効率的に力を伝達し、構造物を支持する。このような軸抵抗する空間構造を対象に力学的合理性に優れた幾何的に性質の良い曲線や曲面構造の設計手法を構築する。これらに加え、建築物に適用されていない幾何的に性質の良い曲線や曲面の利用方法について検討を行う。

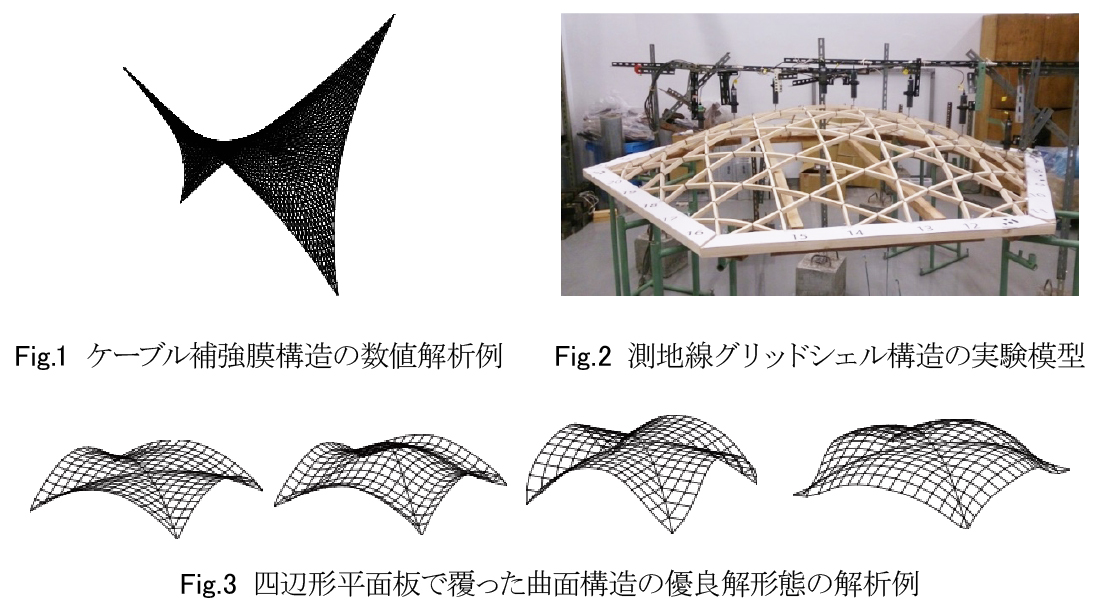
自由な形状を曲面構造のデザインとして採用する場合、施工性に優れた曲面構造が必要となる。測地線を曲線部材として利用すれば、直線部材から空間曲線を構築することが可能であり、平坦な四辺形で覆われた曲面であれば、接合部の簡素化が実現できる。このような幾何的に性質の良い施工性に優れた曲面構造の設計手法を構築する。これらの構成方法に基づき、構造最適化問題と組み合わせることで最終的に力学的合理性+施工性に優れた幾何的に性質の良い構造を実現する。解形態は問題に応じて大域最適解(パレート最適解)や局所最適解(局所パレート解)あるいはそれらを含む比較的評価の高い優良解の範囲まで考慮する。

2. 2.幾何的な汎関数や離散化の有限要素法への応用

曲面の第一基本量は面内ひずみと対応関係があり、弾性係数を用いて有限要素法における汎関数を表現している。極小曲面問題はDirichletエネルギーの最小化問題として定式化することができる。これは、有限要素法における初期張力を一定とした等張力曲面の形状決定問題と等価となる。座標仮定有限要素法や微分形式の新たな離散化手法を用いた有限要素法の定式化を行い、上記1の内容を形状決定問題へ応用することで、座標系に依存しない簡潔な定式化と解析を実現する。

3. 3.折り紙工学における曲線折りの仮設構造物等への応用

折り紙工学における曲線折りの手法による可搬性や剛性に優れた仮設構造物等の提案を行う。災害時は、安全性を確保した仮設テントや住宅を迅速に大量供給する必要がある。曲線折りで形成される曲面による剛性を利用して、仮設テントに適した構造物の形態解析手法と応用可能性を示す。

研究構想における位置づけ

1-1. 可展離散曲面は建築構造物に有用な曲面であることが知られている。そのほかに幾何的に性質の良い曲面を力学的に優位な観点から調べ、有用な離散曲面を列記し構成方法を確立する。参考文献2,10では膜構造の形状解析手法を提案しており、本研究において発展させる。
1-2. 上記1-1と同様に幾何的に性質の良い曲面を施工性の観点から調べる。参考文献6において測地線グリッドシェル構造の形状決定手法を提案しており、本研究において発展させる。
1-3. 上記1-1, 1-2の両方を満たす解や近傍の解(優良解)が必要である。参考文献7,8,9において優良解探索手法の提案や局所最適解活用の実績を示しており、獲得した解形態の最適性や施工性の尺度を明らかにする。
2. 梶原グループとの協働で新たな離散化手法を用い、工学的に汎用性が高い有限要素法に応用することができる。参考文献2において離散微分形式による手法を提案しており、それを発展させる。
3. 可展離散曲面の実用的な構造物の事例の一つとして、防災や安全性の観点から重要視される仮設構造物を挙げている。本研究課題を遂行する協働グループに適した研究内容である。

参考文献

1. 宇都宮尋史, 本間俊雄, 横須賀洋平：Lagrange 未定乗数法を用いたケーブル補強膜構造の形状･裁断図同時解析, 膜構造研究論文集, No.31 (2019) 掲載前
2. 横須賀洋平, 本間俊雄：離散微分形式に基づくケーブル補強膜構造の初期形状解析, 日本建築学会構造系論文集，Vol.83, No.754, pp.1801-1809 (2018)
3. 和田大典, 本間俊雄：構造形態創生法を活用した鉄骨 曲面形態の構造デザイン ―TOTOミュージアムの曲面形状決定と力学検討―, 日本建築学会技術報告集, No.56, pp.117-122 (2018)
4. Y. Yokosuka, T. Honma：Form-finding Analysis for Reversed Hanging Membrane Forms with Constant Force Density, Asian Congress of Structural and Multidisciplinary Optimization (ACSMO), Paper-ID 0188 (2018)
5. 西森裕人, 本間俊雄, 横須賀洋平：自由曲面グリッドシェル構造の部材長一様化と接合角を考慮した形態創生, 日本建築学会構造系論文集, Vol.81, No.721, pp.565-574 (2016)
6. Y. Yokosuka, T. Honma：Geodesic Search on Triangle Mesh for Frame Structures, Proceedings of the International Association for Shell and Spatial Structures Annual Symposium (IASS), Paper-ID 1461 (2016)
7. N .Tanaka, T. Honma, Y. Yokosuka：Structural Shape Optimization of Free-Form Surface Shell and Property of Solution Search Using Firefly Algorithm, Journal of Mechanical Science and Technology, Vol.29, No.4, pp.1449-1455 (2015)
8. 永田洸大, 本間俊雄：優良解探索群知能による自由曲面シェル構造の多目的最適化, 日本建築学会構造系論文集, Vol.78, No.690, pp.1429-1437 (2013)
9. 本間俊雄, 野瑞憲太：解の多様性を考慮した遺伝的アルゴリズムによる構造形態の創生, 日本建築学会構造系論文集, No.614, pp.35-43 (2007)
10. 本間俊雄, 合田雄策, 安宅信行：座標値を未知量とした有限要素技術による張力構造解析の一方法, 日本建築学会構造系論文集, No.602, pp.161-169 (2006)